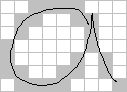
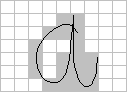
Coding the InputIt is important to the success of a neural network that the input signals fed to it are in an appropriate form. Some thought has to be given as to whether the input can be "coded", i.e. transformed from the form in which it appears in the outside world into some more logical form in which patterns may be more obvious. Here are two commonly used examples: I am often asked how a neural network can be used to recognise handwritten text. Since handwritten text takes the form (usually) of dark marks on white paper, the most obvious way of presenting it to a neural net is as a rectangular grid of pixels. The two grids below illustrate this for two versions of a handwritten letter "a".
To a human eye, these are both clearly letter "a"s, but they translate to different sets of pixels. To a certain extent, this is due to the crude scaling of the pixel elements themselves, but a similar problem might exist in a real system. This shows that a rectangular grid of pixels isn't the best way of representing handwritten text. All right, then, what could we use? Well, let's think about what handwriting is for a moment. You press the pen nib to the paper and then move it continually, tracing out a path. At various points, say at the end of a word or at the end of some letters, you have to lift the pen nib and then put it down again in a nearby position, usually slightly to the right of where you lifted it (if you are using the western alphabet. It would be slightly different for Arabic or Chinese writers who don't move from left to right).
Now the two letters can be translated into a series of numbers:
Now features start to appear. I have colour-coded patterns of digits common to both sets of numbers. 687 represents the top-left curve of the "a", 6654 the bottom-left curve, 223 the rising line just after the bottom of the letter, and 2666 the sharp spike on the right together with its down-stroke. The fact that the two strings of digits are different lengths is a problem, and there is also the problem that the neural net needs to know in which pixel the vector sequence is supposed to start, but at least the representation of the letter is improved. The second example is simpler, but only if you can read music! A musician will tell you at a glance that the two snippets shown below basically represent the same tune - it is the first couple of bars of "Ba, Ba, Black sheep" in fact!   The only difference between the snippets is that the second one has been moved up one semitone, i.e. it is in D flat, rather than in C. However, this transposition means that the two versions only have one note in common! The secret in this case is to represent the tune as a series of note changes, i.e. how many semitones each note is above or below the previous note. If the tune goes up by one semitone, this would be represented by +1. A drop of two semitones would be -2 etc. Each of the tunes could then be represented by two lists, identical for each version.
(There is no pitch difference for the first note as there is no previous note to which to compare it.) I have added a Rhythm line to indicate the length of the notes. This same pattern would represent this tune regardless of its key. Two-dimensional inputsIn many cases, a neural network will be required to recognise a two-dimensional set of inputs, typically an image of some sort. In some specialised cases, such as the handwriting example above, a natural way of representing the input in an intelligent way presents itself. However, in most cases, there is no alternative but to present the image as a series of input values. The most obvious way of doing this is to make all the functions that we have come across so far two-dimensional as well. Here, for instance, is the function for running the input layer of the network (compare it with the one-dimensional version that you met before):
function run_input_layer ()
{ var i,j,x,y;
for (x = 0; x < NUM_INP_ROWS; x++) // Go through all input layer neurons
for (y = 0; y < NUM_INP_COLS; y++)
{ var total = 0;
for (i = 0; i < NUM_INP_ROWS; i++) // For each neuron, go through all inputs
for (j = 0; j < NUM_INP_COLS; j++)
total += i_w[i][j][x][y] * inputs[i][j];
i_out[x][y] = transfer(total - i_thresh[x][y]);
}
}
Suddenly the number of subscripts on all the arrays has doubled. In this case, the inputs are in array inputs[i][j] which has NUM_INP_ROWS rows and NUM_INP_COLS columns. In this particular example, I am assuming that the neurons in the input layer are also arranged in a rectangular format, so that the thresholds for input layer neuron x,y are i_out[x][y] and i_thresh[x][y] respectively, and the weights from input i,j to input layer neuron x,y are (deep breath, now) i_w[i][j][x][y]. for loops that go through all the inputs and input layer neurons have become double for loops nested within one another. Of course, you can simplify the process considerably by keeping the neural network itself as one-dimensional, in which case you would need two variables for the inputs themselves, but only one for the neurons in the input layer (and beyond):
function run_input_layer ()
{ var i,j,x;
for (x = 0; x < NUM_INPUTS; x++) // Go through all input layer neurons
{ var total = 0;
for (i = 0; i < NUM_INP_ROWS; i++) // For each neuron, go through all inputs
for (j = 0; j < NUM_INP_COLS; j++)
total += i_w[i][j][x] * inputs[i][j];
i_out[x] = transfer(total - i_thresh[x]);
}
}
This is a hybrid version of the two-dimensional version directly above and the simple one-dimensional version that you met a few pages back. In this case, NUM_INPUTS refers to the number of input layer neurons rather than the number of inputs themselves. We only need one variable (x) to scan through all the input layer neurons. The inputs, on the other hand, are still in the two-dimensional array, and require two variables (x and y) to scan through them. Of course, the ultimate (and obvious) step is to carry out a function before any of the training or running of the network, which takes the two-dimensional input and puts it in a one-dimensional array:
function convert_input ()
{ var i,j,index = 0;
for (i = 0; i < NUM_INP_ROWS; i++)
for (j = 0; j < NUM_INP_COLS; j++)
{ new_inputs[index] = inputs[i][j];
index++;
}
}
In this case, the input is recast into a new array, new_inputs, which is one-dimensional, and all running and training of the network can be based on that. |
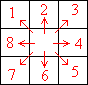 A better way of encoding this is as a series of vectors, i.e. numbers describing the movement of the nib, specifically which direction it is going in at any time. Wherever the nib is at any point (i.e. whichever pixel it occupies), it can move in one of 8 directions, as shown.
A better way of encoding this is as a series of vectors, i.e. numbers describing the movement of the nib, specifically which direction it is going in at any time. Wherever the nib is at any point (i.e. whichever pixel it occupies), it can move in one of 8 directions, as shown.
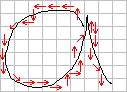 I have labelled each vector with a number from 1 to 8, to which we can add a vector labelled 0 to indicate that the line stops (i.e. the nib is lifted from the paper). Here is the first letter "a" above marked with these vectors.
I have labelled each vector with a number from 1 to 8, to which we can add a vector labelled 0 to indicate that the line stops (i.e. the nib is lifted from the paper). Here is the first letter "a" above marked with these vectors.