Multi-Layer PerceptronLinearly Inseperable Problems
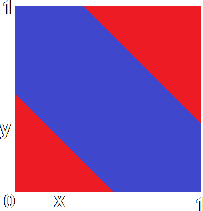
The problem is that a single layer perceptron (SLP) can't produce such a division of the input space, since it is impossible to draw a straight line through that input space with the red region entirely on one side and the blue region entirely on the other. This problem and countless variations on it are generally called the Exclusive OR problem, referring to the Exclusive OR (XOR) function in digital electronics, which produces an output if either one of its inputs is true but not both.
The diagram on the left shows the MLP for the two-dimensional XOR problem shown above - an SLP containing two neurons and feeding into a single neuron that produces the single 1 or 0 output, and the JavaScript code for the network is in this textarea:
Want to try it without all that "Copy and Paste" nonsense? Go ahead: You will notice that some of the weight and threshold values are negative. I did say that they didn't have to be limited to the range 0 to 1. If you want to know how I calculated the values, click here. 
The General MLPOf course, that was a very simple MLP (probably the simplest that you can get). A more general one would have several neurons in both the input layer and the output layer, as shown in this diagram. Such a network would probably be referred to in the literature as a 2-layer network. I say probably, as some researchers refer to the set of inputs themselves as a layer, even though they are just points in the network where the input signal appears rather than neurons themselves, and so they call that network a 3-layer network.
The second layer of neurons is called the hidden layer, as neither the inputs of those neurons nor their outputs are connected to the "outside world". The outputs of the input layer neurons feed into the hidden layer, and the outputs of the hidden layer neurons feed into the output layer. ... And now for some code!From here on, I shall adopt a couple of conventions:
When you look at the code you will see that it consists of three almost identical functions, one for each layer. The run_input_layer() function takes the input values and multiplies them by the weights on the input layer to produce an output for the inner layer. The run_hidden_layer() function takes the outputs from the input layer and multiplies them by the weights on the hidden layer to produce an output for the hidden layer. The run_output_layer() function takes the output values for the hidden layer and multiplies them by the weights on the output layer to produce a final output for the network itself. To run the network, simply run each of the functions in order. If you wanted to, you could add extra layers by putting in similar weights, thresholds and output values plus an extra function for that layer, though you could make your network solve more complicated problems simply by adding more hidden layer neurons. So far we have glossed over a very important aspect of ANNs - How do we set all those weights and thresholds? After all, they form the knowledge in the ANN itself. For a MLP, there is a standard way to set weights and thresholds, the Back Propagation Method, which we shall meet in the next section... |
 You must have realised that there are problems which can't be solved by slicing the input space with a single straight plane, however many dimensions you use. These are
You must have realised that there are problems which can't be solved by slicing the input space with a single straight plane, however many dimensions you use. These are 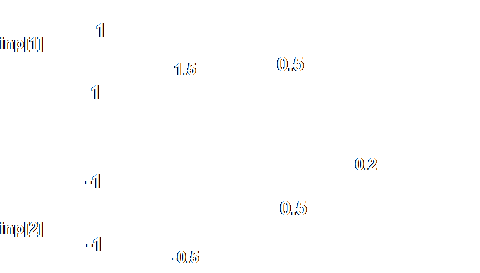 The solution to this problem is to have an SLP divide up the input space as best it can and then have the outputs from that SLP interpreted by another SLP, giving a simple 1 or 0 (yes or no) answer. This SLP-piggy-backed-on-an-SLP arrangement is called a Multi-Layer Perceptron (MLP), and is probably the most common configuration for an ANN.
The solution to this problem is to have an SLP divide up the input space as best it can and then have the outputs from that SLP interpreted by another SLP, giving a simple 1 or 0 (yes or no) answer. This SLP-piggy-backed-on-an-SLP arrangement is called a Multi-Layer Perceptron (MLP), and is probably the most common configuration for an ANN.
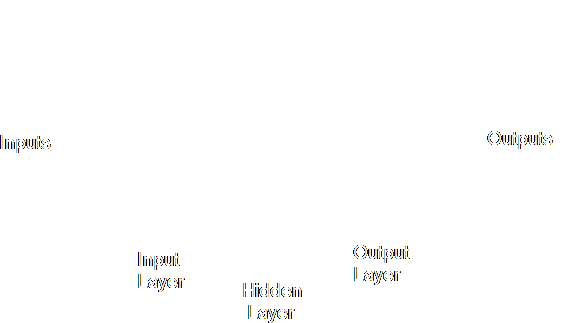 In order to divide the input space in any arbitrary way you want, you need a Multi-Layer Perceptron with three true layers of neurons. It can be shown that the input space (of however many dimensions) can be divided up in as complicated a way as you like if your MLP has three layers - no more are needed (although you can add more layers of neurons if you want) - providing you have enough neurons in each layer, of course (
In order to divide the input space in any arbitrary way you want, you need a Multi-Layer Perceptron with three true layers of neurons. It can be shown that the input space (of however many dimensions) can be divided up in as complicated a way as you like if your MLP has three layers - no more are needed (although you can add more layers of neurons if you want) - providing you have enough neurons in each layer, of course (