Calculating Weights and Thresholds for XORnet

With a linearly inseparable problem as simple as this one, it is fairly easy to get the connection strengths and thresholds by hand-crafting them. Later on, I will describe a procedure that lets you calculate the weights automatically for much larger problems.

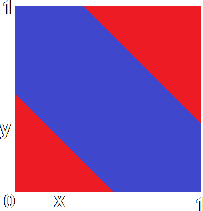
Look at that input space again. It consists of two red regions divided by a blue region. If the combination of inputs falls into either of the two regions, then the ANN should produce a 1 output. Otherwise, it should produce a 0 output:

Þ

OR

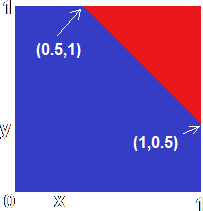Now consider that upper red region. I have arbitrarily decided that it should run through the points (1,0.5) (i.e. where the first input has the value 1 and the second the value 0.5) and (0.5,1) as shown. A little bit of fairly simple mathematics tells you that the equation of the dividing line between red and blue is x + y = 1.5. For all the points in the red region, x + y ³ 1.5 and for all the points in the blue region, x + y < 1.5.

We want a neuron in the circuit to produce a 1 output when it detects a point in the red region, so x + y ³ 1.5, where x and y are the weighted inputs. You can see that this is easily achieved by taking each input, multiplying it by a connection strength of 1 (i.e. leaving it unchanged) and then comparing the weighted total with a threshold of 1.5. This produces a neuron with the parameters shown on the right. Of course, the same could have been achieved by multiplying each input by a connection strength of 0.5 and comparing the weighted total with a threshold of 0.75, or countless variations on that. However, I prefer to something simpler if possible.

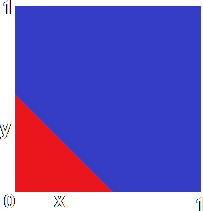
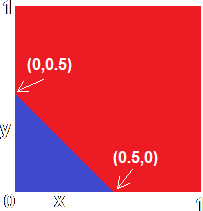What about the lower region. Well, in a similar manner, I have decided that the dividing line between them should go through the points (0,0.5) and (0.5,0) giving an equation x + y = 0.5. We could create a neuron with weights of 1 and a threshold of 0.5, in a similar way to the neuron above, but that would give divide the input space so that the neuron produced a 1 output when the total weighted input went above 0.5 instead of below it, i.e. the region in red shown on the left.

We could, of course, alter the model of the neuron so that it fired when the total weighted input went below the threshold. However, that is a clumsy and unsatisfactory thing to do, and there is a way to get round it without having to compromise our model. Make the weights both -1 and the threshold -0.5, so that the total weighted input is (-x) + (-y) and the neuron produces 1 when that total weighted input goes above the threshold: (-x) + (-y) ³ -0.5. We can multiply that inequality by -1, in which case the inequality sign is reversed: x + y £ 0.5 - bingo!

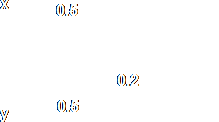Now we have two neurons that each produce a 1 when the combination of inputs is in one of the two red regions. Up to this point we could have just used an SLP - two neurons as described sitting next to each other and feeding off the same pair of inputs. However, we want our network to produce a simple 1 or 0 output representing red or blue. so we introduce another layer of neurons - well one neuron actually - which recognises when either of the two neurons below it produces a 1 and signals a 1 in turn. This couldn't be simpler. We simply multiply each of the inputs to this neuron (which are the outputs of the two previous neurons - try to keep up!) by a value such as 0.5 and then set the threshold so that any non-zero combination of inputs will trigger a 1 (I've chosen 0.2 as an arbitrary figure). If either of the two inputs is non-zero, the neuron produces a 1. If both the inputs are 0 (i.e. the combination of inputs is in the blue zone), then the final neuron will produce 0.

I suggest you take each of the neurons described here and compare them with the parts of the network on the main page to see how they fit in.