Moles and the Avagadro Constant

What is the Avagadro Constant?

If you have a dozen ping-pong balls, it means you have 12 of them. Similarly, if you have 20 ping-pong balls, it's called a score. 144 nails is called a gross. The Avagadro constant is similar to these - it is simply a number, albeit a very big one. The value of the Avagadro constant is 6.02 x 10²³ (approximately equal to a 6 with 23 noughts after it).

(In most chemistry questions, you can take the Avagadro constant as being 6 x 10²³, and forget about the .02 on the end!)

This number is special because it is the number of carbon atoms that makes exactly 12 grammes of carbon, i.e. if you had 6.02 x 10²³ carbon atoms on a scale, it would read exactly 12 grammes. Although the Avagadro constant is officially defined in terms of carbon, it is probably easier to think of it in terms of the simplest atom, hydrogen.

6.02 x 10²³ hydrogen atoms have a mass of 1 gramme. This means that the mass of one hydrogen atom must be 1/(6.02 x 10²³) of a gramme. We refer to 6.02 x 10²³ hydrogen atoms as a mole of hydrogen atoms. Similarly, if you had 2 grammes of hydrogen, that would be two "Avagadro constant's worth", in other words 2 moles of hydrogen atoms.

Similarly, 3 grammes of hydrogen is 3 moles of hydrogen atoms and 17.361 grammes of hydrogen is 17.361 moles of hydrogen atoms. It gives you a convenient way of counting atoms.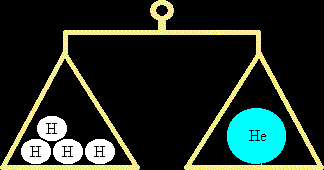

Relative Atomic Mass

Every atom has a relative atomic mass (R.A.M.) which tells you how heavy the atom is when compared to hydrogen. For instance, every helium atom is 4 times as heavy as a hydrogen atom. Helium has a R.A.M. of 4. (Actually, not every atom of helium is exactly 4 times as heavy as hydrogen as various isotopes of helium exist, such as helium-3, but they are sufficiently rare that we can ignore them).

So how much would a mole of helium atoms weigh?

Well, if a mole of hydrogen atoms has a mass of 1g, and helium atoms are 4 times as heavy as hydrogen atoms, then a mole of helium atoms must be 4g (4 times as much as for hydrogen). Similarly, 2 moles of helium atoms would be 8g (twice 4g), 10 moles of helium atoms would be 40g (ten times 4g) etc.

What about other elements? Take oxygen for example. This has a Relative Atomic Mass of 16, meaning that each oxygen atom is 16 times as heavy as a hydrogen atom. One mole of oxygen must be 16g. 3 moles of oxygen must be 3 x 16 = 48g etc.

In short, if you know what the R.A.M. of an element is, then you can find the mass of one mole of the element is by slapping 'grammes' on the end of that figure. If you want the mass of a different number of moles (16 moles, 23.5 moles etc.) then multiply the mass of one mole by that figure.

Suppose you have the number of grammes of an element and you want the number of moles that are present. In this case, you do the opposite - you divide by the R.A.M., so 48 grammes of oxygen contains 48 / 16 = 3 moles of oxygen. Since the R.A.M. of mercury is 200.6, then 500 grammes of mercury must contain 500 / 200.6 = 2.492 moles of mercury.

The basic formula is:

Of course, the formula can be turned round:

or even:

Exercise 1

(You will need some relative atomic masses to do these questions: Iron = 56, Uranium = 235, Chlorine = 35.5, Silicon = 28, Sodium = 23, Nitrogen = 14).

Relative Atomic Masses given as decimals

If you check in any chemistry reference book, you will see that relative atomic masses are always quoted as figures to a certain number of decimal places. Compare the figures I gave you for the relative atomic masses of various elements in Exercise 1 with the figures that the reference book gives you:

So what's going on? Well, the unfortunate truth is that the atoms of each element take the form of various isotopes, which means that they have the same number of protons in each atom but different numbers of neutrons. I won't go into great detail here as there is a different section that explains it better, but suffice it to say that while the great majority of atoms of any element are the same number of times heavier than hydrogen as I told you, some aren't.

Yeah, I've just re-read that sentence and you're right. It does need a great deal of explanation. Let's take Iron (symbol Fe) as an example. There are four isotopes of iron that exist in nature (you could probably make more if you cranked up the atom-smashing machines to full volume): Fe-54, Fe-56, Fe-57 and Fe-58. In case you're interested, an Fe-54 atom has 26 protons and 28 neutrons (26 + 28 = 54), an Fe-56 atom has 26 protons and 30 neutrons (26 + 30 = 56), an Fe-57 atom has 26 protons and 31 neutrons and an Fe-58 atom ... well, I'll let you work that one out for yourself.

You've spotted that every single iron atom has 26 protons, right? Well, that's what makes it an iron atom. If it had more protons or fewer, it wouldn't be iron, it would be something else. However, it's the number of neutrons that create the different isotopes. So when we "weigh" an iron atom against a hydrogen atom, we're really weighing protons and neutrons.

The trouble is that all these isotopes are mixed up in nature. There's no way we can get, say, an iron nail and guarantee that it has only one isotope of iron in it (or even remove one of the isotopes out of the nail at all). Chemically, all these atoms of iron react the same way, so there's no chemical procedure we can use to separate them. This means that when it comes to relative atomic mass, they're a fact and we have to deal with them.

However, take a look at these relative abundances of iron isotopes in the world around us:

The great majority of iron atoms (more than nine out of ten) are Fe-56, so we can say "stuff it, let's call the relative atomic mass 56" and this is close enough to be used in most calculations. In fact, if you were to produce a weighted average for the figures, you would get the relative atomic mass quoted in the reference book:

So what about the relative atomic mass of chlorine? Even before you tried exercise 1, I had given that as a decimal. Well, there are two common isotopes of chlorine, Cl-35 and Cl-37, and the proportions are such in nature that the weighted average comes out at approximately 35.5. Try as they might, they just can't justify panel beating that to either 35 or 36, so we just have to shrug and call it 35.5.

There is one exception that will jump out at you as you cast your eye down the reference table. The relative atomic mass of carbon is given as exactly 12, i.e. 12.000000. Now, there are at least two isotopes of carbon that I know of, C-12 (twelve times as heavy as hydrogen) and C-14 (fourteen times as heavy), so surely it should be some sort of decimal. Well, yes... but the exact figure comes from the way the Avagadro constant is defined. Since by definition, there are one Avagadro number's worth of carbon atoms in exactly 12g of carbon, then the R.A.M. must come out as exactly 12. Basically, all those different isotopes have been taken into account when the figure of 6.02 x 10²³ was decided upon. (Besides, the vast majority of carbon atoms are C-12 anyway, so it makes almost no difference!)

Relative Molecular Mass

Of course, it may not be simple elements that you are dealing with. You may find that it is a compound (more than one element chemically joined together). Let's suppose you want to find the mass of one mole of iron sulphide (FeS).

One molecule of iron sulphide consists of one atom of iron chemically bonded with one atom of sulphur - they join on a one-to-one basis. It therefore follows that one mole of iron sulphide must contain one mole of iron atoms joined to one mole of sulphur atoms.

One mole of iron atoms = 56 grammes (as the R.A.M. of iron is 56).

One mole of sulphur atoms = 32 grammes (as the R.A.M. of sulphur is 32), so ...

One mole of iron sulphide = 56 + 32 = 88 grammes. Similarly, two moles of iron sulphide are contained in 2 x 88 = 176 grammes, and 4 moles in 4 x 88 grammes etc. After that it is exactly the same as what you met up above.

So, to find the Relative Molecular Mass (not Atomic - we are dealing with compounds here), just add the R.A.M. values for the atoms that make up the molecule. You must be careful to add them in the correct proportion - there may be more than one atom of an element in a compound.

For instance, glucose has a chemical formula of C₆H₁₂O₆, where carbon has a R.A.M. of 12, oxygen has an R.A.M. of 16 and hydrogen has an R.A.M. of 1. To find the R.M.M. of glucose, you don't just do 12 + 16 + 1, because there are 6 carbons in there, 12 hydrogens and 6 oxygens. The final calculation is:

• 6 x 12 for the carbon = 72
• 12 x 1 for the hydrogen = 12
• 6 x 16 for the oxygen = 96

The R.M.M. of glucose is 72 + 12 + 96 = 180. This means that one mole of glucose is 180 grammes, half a mole would be half of 180 = 90 grammes, eleven moles would be 11 x 180 = 1980 grammes (or 1.98 kilogrammes) etc.

Exercise 2

For this exercise, you will need to use the R.A.M. values specified below:

Molarity and Titration

Many substances dissolve in water. The concentration of any substance, its molarity, is usually calculated in terms of how many moles of the substance are dissolved in one litre of water. The units are moles/litre, or more recently, moles/dm³, since one dm³ (one cubic decimetre) is the same as one litre. This doesn't mean that you have to have exactly one litre of solution, it just gives a measure of how much substance would be dissolved in one litre of water if you had a litre with the same concentration.

Perhaps an example would clear this up. Suppose we had exactly 29.25g of sodium chloride. If you do the calculations you will see that this is exactly half a mole. We then dissolve this sodium chloride in 200cm³ of a litre of distilled (totally pure) water. This means that we have half a mole of salt dissolved in 0.2 of a litre, which is the same concentration as if we had 2.5 moles dissolved in 1 litre. We therefore say that the concentration of the solution is 2.5 Molar (or 2.5M), even though we only have one fifth of a litre.

To calculate the concentration of any solution, divide the number of moles of substance by the volume of water in litres (dm³). Here is another example:

Dissolve 34.11g of sodium hydroxide (R.M.M. = 40) in 30cm³ of distilled water. 34.11g is 34.11 / 40 = 0.85275 moles of NaOH dissolved in 0.03 litres of water, so the concentration is 0.85275 / 0.03 = 28.425 Molar. That's very concentrated! Typically, you won't come across concentrations much higher than 2M.

The basic formula is:

Of course, the formula can be turned round:

or even:

So what's titration then? It is the process of working out the concentration of a solution by reacting it with a solution of known concentration. This is often (almost always) done with acids and alkalis. Let me explain with an example: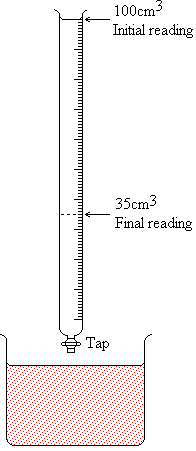

Suppose we have a sample of sulphuric acid (H₂SO₄) of unknown concentration in a flask, but whose volume is known accurately. We set up a burette (a long thin graduated tube with a tap at the base) above it and fill it to a certain graduated mark with sodium hydroxide solution of concentration 0.5M, as shown in the diagram on the right.

Then we put some litmus solution in the acid - it goes red, of course. This litmus will tell us when enough of the sodium hydroxide has reacted to neutralise the acid. We gradually let the sodium hydroxide run into the acid by opening and closing the tap on the burette. The flask is gently swirled after each part of the hydroxide has been let in, and the colour carefully noted. The swirling is necessary to make sure that the solutions are thoroughly mixed - you will find a dribble of blue appears as you let the hydroxide in, but that the litmus goes back to red as you swirl.

Eventually, even with swirling, you notice that the colour is starting to change. This is the point to let the hydroxide in one drop at a time, until you are sure that all the red colour has disappeared. At this point, the reading on burette is noted again.

It would help if we put some figures in this example:

The balanced chemical equation for the neutralisation of sodium hydroxide with sulphuric acid is as follows:

The important thing to note here is the left side of the equation: It takes 2 moles of sodium hydroxide to neutralise 1 mole of sulphuric acid. However, we don't have 2 moles of sodium hydroxide, we only have 0.0325 moles. This will neutralise half as many moles of acid:

We have finally calculated the concentration of the acid.

Erm ... Could you explain that bit about the correct proportions of acid and alkali again?

Here you have the balanced equation for hydrochloric acid neutralising sodium hydroxide. Check it is balanced for yourself. You can see that there is one molecule of hydrochloric acid on the left side of the equation and one mole of sodium hydroxide on the left, so it takes one mole of hydrochloric acid to neutralise one mole of sodium hydroxide completely:

Similarly, 0.1 moles of hydrochloric acid neutralise 0.1 moles of sodium hydroxide, 237.4 moles of acid neutralise 237.4 moles of hydroxide etc. They always react in a 1 : 1 ratio. N.B. The same isn't true of volumes! You can't assume that 1 litre of hydrochloric acid neutralises 1 litre of hydroxide - that depends on the concentration of the chemicals as well!

Surely it isn't that simple!

Well, no it isn't! This, for instance, is phosphoric acid neutralising sodium hydroxide. Again, it is a balanced equation:

In this case, it takes 3 molecules of sodium hydroxide to neutralise every molecule of phosphoric acid. This means that you would need 3 moles of hydroxide to neutralise 1 mole of the acid, or 0.9 moles to neutralise 0.3 moles of acid etc. In this case, the chemicals react in a 3 : 1 ratio.

For each reaction, you should write a balanced equation. Then decide on the ratio of the reactants that neutralises them exactly.

Go back