The Hopfield Net

The Hopfield Net is a neural network that is a lot simpler to understand than the Multi Layer Perceptron. For a start, it only has one layer of nodes. Unlike the MLP, it doesn't make one of its outputs go high to show which of the patterns most closely matches the input. Instead it takes the input pattern, which is assumed to be one of the library patterns which has been changed or corrupted somehow, and tries to reconstruct the correct pattern from the input that you give it.

These library patterns are also called attractor states, because if you give the network some input, it will gradually alter its internal conditions until it is in one of these states (we hope, see below). We say that the network is attracted to one of the states. Here's what I mean. Suppose you have trained your Hopfield Net on these patterns:

You present a pattern which is a bit like one of them and leave the net to run. It gradually alters the pattern you give it until it has reconstructed one of the originals:

The Hopfield Net is left to iterate (loop round and round) until it doesn't change any more. Then it should match one of the input patterns. The program should then compare the reconstructed pattern with the library of originals, and see which one matches. In this way, the Hopfield Net forms a content addressable memory - you give it part of a library pattern that may have been corrupted, and it reconstructs the original for you.

However, the Hopfield Net is not guaranteed to converge on any library pattern at all. Sometimes it just goes round and round through a sequence of patterns that don't match any of them. If you hand-craft the data well, it should converge on a pattern.

Hopfield nets rely on binary inputs. The inputs are either 1 or -1 rather than 1 and 0. Any other inputs patterns must be converted to 1s and -1s first. Here's the structure of a Hopfield Net:

OUTPUTS (Valid after convergence)

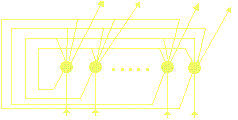
INPUTS (Applied at time zero)

The inputs to the Hopfield Net are at the bottom. The nodes produce an output which comes out at bottom and is fed back into all the nodes except the one that produced it (i.e. all the nodes refer to each other, but not to themselves) and uses this to produce the next output. The final output of the nodes is extracted at the top.

The nodes themselves are defined by the connection weights (called t) and the hardlimiting function. This takes the input and gives either 1 if it is positive, or -1 if it negative. The connection weights are set up at the start based on the library patterns themselves.

var PATTERN_LENGTH = 8;  // The number of elements in the pattern
var t = new Array();
for (var i = 0; i < PATTERN_LENGTH; i++)
  t[i] = new Array();
// t[i][j] = connection weight from node i to node j
// Both indices run from 0 to PATTERN_LENGTH - 1

If t_ij is the weight from node i to node j then it is defined as follows:

• If i = j, the weight is 0 (i.e. there is no weight from any node to itself).

• If i is not j, the weight is a sum of multiplications, as follows:

  M
  S	xsi.xsj
  s = 1

  where x^s_i is the element number i of library pattern s (with value either 1 or -1) and x^s_j is the element number j of library pattern s (again either 1 or -1). The sum is done over all the M library patterns.

What this means is: "For every pair of inputs i and j (apart from each input to itself) do the following: Go through all the library patterns, and multiply the corresponding elements (x_i and x_j) for that pattern. The t value for i to j will be the sum total of all those multiplications."

Here's the JavaScript code that does the same thing:

function assign_connection_weights ()
{ for (var i = 0; i < PATTERN_LENGTH; i++)
   for (var j = 0; j < PATTERN_LENGTH; j++)
    if (i == j)
      t[i][j] = 0;
    else
      { var sum = 0;
        for (var s = 0; s < MAX_CLASSES; s++)
          sum += x[s][i] * x[s][j];
        t[i][j] = sum;
      }
}

Hopfield proved that providing that these t values are symmetrical (i.e. t_ij is always the same as t_ji), then the network is guaranteed to converge on some pattern (although not necessarily one of the ones in the library of patterns). Isn't he a clever bloke!

The outputs of the net are stored in an array called m ("mu"). This has the same number of values as there are elements in the patterns, and changes from one time slot to the next. m_j(t) is the value of output j at time t (not to be confused with the weights, which are also referred to as t in the literature).

The unknown input pattern is copied into time slot 0:

var MAX_TIME = 10;   // Maximum no. of time slots before convergence

var mu = new Array();
for (var t = 0; t < PATTERN_LENGTH; t++)
  mu[t] = new Array();
// mu[t][i] = value of node i at time t

function copy_input_pattern ()
{ for (var i = 0; i < PATTERN_LENGTH; i++)
    mu[0][i] = input_pattern[i]      // Each element +1 or -1
}

The iteration works as follows. The weights are multiplied by the previous m values, then totalled and passed through the hard-limiting function that reduces the values to 1 or -1. These values then become the m values for the next time slot. After a while (hopefully) the m values converge on one of the library patterns:

function iterate ()
{ var tt;     // Time slot
  for (tt = 0; tt < MAX_TIME; tt++)
   for (j = 0; j < PATTERN_LENGTH; j++)
    { var sum = 0;
      for (var i = 0; i < PATTERN_LENGTH; i++)
        sum += t[i][j] * mu[tt-1][i];
      // Now pass sum through the hard-limiter, so it is 1 or -1
      if (sum > 0)
        mu[tt][j] = 1;
      else
        mu[tt][j] = -1;
    }
}

This is a simple one-dimensional Hopfield net. There are four training patterns, each with 8 bits, and a test pattern. The fact that there are so many training patterns compared to the number of bits means that the Hopfield net is rather overloaded! You may find that some training patterns that you specify don't actually converge on a library pattern, but oscillate repeatedly.

If you click on the button marked "View Training Patterns", then you will see the built-in training patterns. You can alter these by clicking on the black and white circles. Every time you click on a training pattern, the net is retrained automatically. Click on the button marked "View Main Screen" to return to the main screen.

Similarly, you can set up a test pattern by clicking on the white circles that make the pattern up. The button marked "Single Step" is used to run the net according to the rules given above. Each time you click on the button, one iteration of the loop takes place. If you want the pattern that is generated to settle down, then click on the button several times (although, you will probably find that it settles down into the nearest pattern almost immediately!)

The black circles represent the number +1 in the Hopfield net, the white circles -1. If you look at the source code (which you are free to do with as you like, of course), you will see that I don't have an array called "mu" (unlike the JavaScript code above). Instead, the initial pattern is called "testPattern" and this is updated after each run of the loop. However, this array has exactly the same role as the array "mu" in the original.

You will find that this net does tend to oscillate, especially if you blacken only two circles of any training pattern. If you want to be sure of correct pattern completion, you should leave all the circles white except three of any training pattern. The net should then fill in the missing fourth circle.

Another demonstration Hopfield Net