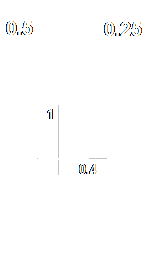
The Single Layer Perceptron and Linearly Separable ProblemsBelow you will see a simple neuron with only two inputs and a step transfer function. I have set the weights on the inputs to 0.5 and 0.25 and the threshold to 0.4, but you can set the input values for yourself. You can think of the two inputs as x-y co-ordinates on a two-dimensional grid, and I have placed a grid next to the neuron to display the results. Every time you select a pair of input values and click on Process, a point will be marked on the grid corresponding to the two inputs. If the neuron produces 1 for that combination of inputs, the point will be marked with a red circle, if 0, with a blue circle.
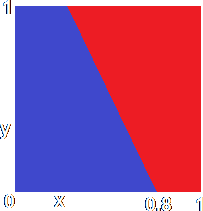
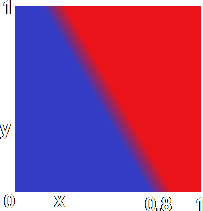
You will notice that all the red dots (the combinations of inputs producing a "1" output) lie on one side of a straight sloping line, and all the blue dots (the combinations producing a "0" output) lie on the other side. It wouldn't make much difference if the neuron used the sloping transfer function or the sigmoidal one. In these cases, there wouldn't be a sharp distinction between 0 on one side of the line and 1 on the other, but a gradual increase in the output value (if you like a "blend" from blue to red). However, the rise from 0 to 1 would still occur across the same line - a rather fuzzy one in this case.
It's a little hard to see when the sigmoid function is used, but that dividing line is still there. This graph is called a two-dimensional input space as it can be represented using a two-dimensional graph. The two outputs of the network are referred to as linearly separable as you can separate the 1s from the 0s by a single straight line (however fuzzy). Altering the threshold and the weights (perhaps making them negative or larger than 1) would alter the position and slope of that dividing line, but the outputs would remain linearly separable as it would always be possible to draw a single straight line between the 0s and the 1s on the graph.
We can go further an imagine the input space for a 4-input, 5-input etc. neuron. In this case, we would need a 4-dimensional input space, or 5-dimensional etc. so we can't draw it in a diagram, but the same principal applies - the neurons would separate the multi-dimensional input space into two regions using a multi-dimensional plane. All such input spaces are called linearly separable. 
The Single Layer PerceptronLet's expand from one single neuron to several put side-by-side. They all share the same inputs, and each produces one output, as shown in this diagram. This is called a Single Layer Perceptron. Each neuron is connected to all the inputs, and each subdivides the (in this case) 4-dimensional input space according to its own particular plane, depending on its particular weights and threshold, and what you end up with is 4 output numbers. Between them they can describe the input space in a far more complex manner than a single neuron. The problem is then interpreting the outputs of the neuron ... and for that you need an extra layer of neurons. Wheel on the ... (drumroll!) ... Multi-Layer Perceptron! Here is some JavaScript code for a single layer perceptron. We'll assume that there are NUM_INPUTS inputs and NUM_NEURONS neurons. I haven't put in the code for setting up the arrays of inputs, weights and thresholds, but we'll assume that inp[i] contains the value of input i, w[i][j] is the weight from input i to neuron j and thresh[j] contains the threshold for neuron j. To copy all the code into the clipboard, click on the button marked "Copy". Then paste it into a text editor such as Notepad so that you can save/edit it. If you examine the code above, you will notice that it is basically the same as the code on the previous page except duplicated for all the neurons in the SLP. The array of weights now has to be 2-dimensional, as it contains the weights from all the inputs to all the neurons, and the single threshold value of the previous page now becomes an array of threshold values (one for each neuron). The output values for the neurons end up in the array out[] - what you do with them is up to you, of course. | ||||||||||||||
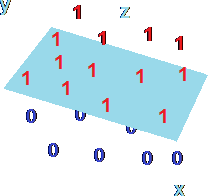 Suppose we had a neuron with three inputs, not two. In this case, the input space would be three-dimensional, with the inputs themselves represented by the x-, y- and z-axes. The space would still be linearly separable, as it would be possible to draw a flat plane (the 3D equivalent of the dividing line) through the space with all the 1s on one side and all the 0s on the other.
Suppose we had a neuron with three inputs, not two. In this case, the input space would be three-dimensional, with the inputs themselves represented by the x-, y- and z-axes. The space would still be linearly separable, as it would be possible to draw a flat plane (the 3D equivalent of the dividing line) through the space with all the 1s on one side and all the 0s on the other.