The Neuron (real and artificial)Real neuronsThe human brain is made up of a large number of brain cells, or neurons. Estimates of the number of neurons in the brain vary from between about 109 and about 1011 (Hubel and Wiesel, 1968, Sholl, 1956, Williams and Herrup, 2001). Working together in large numbers, these neurons result in everything from keeping your breathing going automatically, to human thought and consciousness. Having said that, each neuron is itself fairly simple. It essentially acts as a switch, taking in input signals in the form of electro-chemical reactions, and amassing them, and then producing an output when it has built up enough energy. We say that the neuron builds up a chemical charge as a result of the incoming signals, and then fires when the charge it has built up goes above a certain level or threshold.
The connections between neurons are referred to as synapses or synaptic connections. Each synapse has a certain strength or weight, indicating how easily the signal can transfer across the connection. A high weight or strength indicates a good connection, so that a greater proportion of the signal manages to cross the gap. A low weight or connection strength indicates that the synapse is not good at passing the signal across. The input to the brain cell comes in from many synapses at the end of long filaments called dendrites. The chemical charge is built up in the main body of the cell, the soma, and, if the charge is high enough, the neuron fires, by sending an electro-chemical charge down a long output connection, called the axon. This then passes across more synaptic connections to other neurons. Once the neuron has fired, it has discharged and can't fire again until it builds up more charge. The actual information and knowledge is stored in the strength of the connections between the neurons. This pattern of synaptic strengths determines which neurons fire and in which order. Artificial neuronsIn this tutorial, we are interested in simulating large networks of these neurons in a computer in order to get some useful information processing from them. We simulate a neuron by turning it into a mathematical model and then into computer code. The essential parts of the basic neuron are:
Let's imagine that the raw inputs are called x1, x2, x3 etc. up to xN. (There are N of them). The weights are called w1, w2, w3 etc. up to wN. We get the total weighted input by multiplying each input by its weight and adding the products to form a total:
I have called the total weighted input W, and at the end of that equation, I have written it using the "sigma" notation for the more mathematically minded among you. Now we subtract the threshold, usually represented by the Greek letter "theta" (q), and I think I'll call the final result X: X = W - q
Finally we put the result, X, through the transfer function to produce a final output for our neuron. The transfer function ensures that the output will be in the range 0 to 1, in case the output of this neuron is used as an input to other neurons. You can use any transfer function you like, of course, but here are three common ones. I have added some JavaScript code to show you how to create the functions: Step function: If the input to the function is 0 or less, the function produces a zero output. If the input is more than 0, the function produces 1. 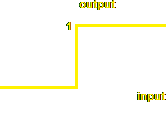
function transfer (inp)
{ if (inp <= 0)
return 0;
else
return 1;
}
Gradual function: If the input to the function is 0 or less, the function produces a zero output. If the input is more than 0, the function produces an increasing value on a sliding scale, with a maximum output of 1. 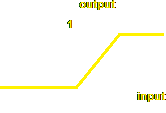
function transfer (inp)
{ var LIMIT = 2; // Some arbitrary limit
if (inp <= 0)
return 0;
else if (inp >= LIMIT)
return 1;
else
return inp / LIMIT;
}
Sigmoidal function: This is probably the most common function, and the one I prefer. It uses an equation involving the exponential function, ex (also written exp(x)) to produce a smooth curve, so that low, negative values of the input produce values close to 0, high positive values of input produce values close to 1, and a 0 input produces an output of 0.5. The equation for the sigmoid function is as follows: 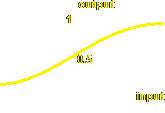
and the code is the function transfer below. Note in that equation (and code), that the input is made negative (-X rather than X). Below I have put the JavaScript code in for a typical neuron.
function transfer (inp)
{ return 1 / (1 + Math.exp(-inp));
}
function neuron (inp)
{ var i, total = 0;
for (i = 1; i <= N; i++)
total += w[i] * x[i]; // Assume weights in w[], inputs in x[]
return transfer(total - threshold);
}
|
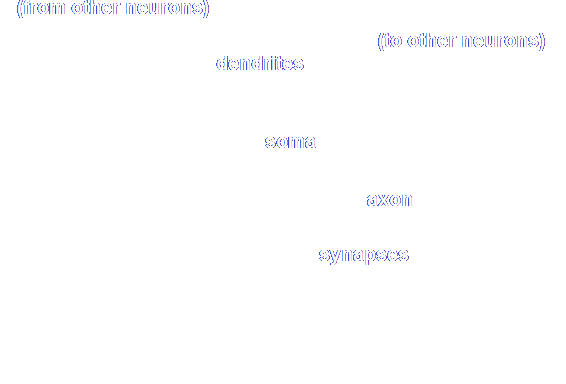 The diagram on the right shows a rough sketch of a neuron, with all the important parts marked. This diagram shows a neuron boiled down to its essentials. In fact, no fewer than 45 different types of brain cell have been discovered (add a reference), all variations on this basic one, but for the purposes of Artificial Neural Networks (ANN), the simple model is sufficient.
The diagram on the right shows a rough sketch of a neuron, with all the important parts marked. This diagram shows a neuron boiled down to its essentials. In fact, no fewer than 45 different types of brain cell have been discovered (add a reference), all variations on this basic one, but for the purposes of Artificial Neural Networks (ANN), the simple model is sufficient.