
Main menu
Glossary of Technical TermsHere are some of the technical terms used a lot in neural network research. Commit a few of these to memory, and not only will you be able to understand what the afficionadoes are blathering about, but you will be able to blather about it yourself! Attractor StatesNeural networks which are recurrent such as Hopfield Nets take in inputs and produce outputs, but also contain signals which go round and round the network internally. We say that the internal signals form a state of the network, and the network moves from one state to another as time goes on. It is possible for states in a recurrent network to be stable, i.e. if the network gets into that state, it will remain in that state (until the program stops, of course). These states are called attractor states - the network moves from unstable states into an attractor state and then stays there, like a piece of iron moving towards a magnet. See also attractor basins Attractor BasinsThis term applies to recurrent networks. Each attractor state has a number of unstable states that will lead to it. If the network is in one of those unstable states, it will inevitably end up in that stable attractor state. The set of unstable states that lead to the attractor state are called its basin.
AutoassociativeA network is described as autoassociative if it associates one input pattern with itself. It is trained on a series of patterns. If the network is then given part of a pattern as input, it can then recreate the complete pattern. See also heteroassociative. Connectionism, ConnectionistConnectionism is the alternative name for the study of neural networks, and connectionists the name for the people that do it. EpochWhen you train a neural network with a library of training patterns, each training pattern has to be presented to the network several (many) times. What normally happens is that the network is shown each pattern once in turn (perhaps in a random order), and then the process repeats many times. Going through all the training patterns once is called an epoch. Training therefore consists of many epochs. Exclusive Or (XOR) ProblemThis is a problem that is often quoted as it involves sets of inputs that are linearly inseparable. Imagine a neural network with two inputs and one output. The two inputs can be either 1 or 0. The network is to be trained so that the output is 1 only if the two inputs are different, as shown in the following table:
Digital electronics students will recognise this as the Exclusive OR (or XOR) function. The reason this problem is so famous is that it was used by Marvin Minsky and Seymour Papert in their famous academic paper Perceptrons as an example of a linearly inseparable problem that could not be solved by single-layer perceptrons. You can train the perceptron as long as you like on the patterns above, and it will still give the wrong answer about half of the time. Ever since then, the XOR problem has been quoted in order to separate the simple neural networks from the more complex ones. Feedforward NetworksNetworks generally consist of layers of nodes or cells. Feedforward nets are those where the signals only travel one way through the net, i.e. having passed from layer x to the next layer up, the signal can't then end up in layer x again. The opposite to feedforward nets are recurrent networks. HeteroassociativeA network is described as heteroassociative if it learns to associate one input pattern with a different input pattern, i.e. it learns to "translate" any input pattern to a different one. If you give it part of any pattern, it will translate that into the different pattern that it corresponds to. See also autoassociative. LearningA neural network learns when it adapts its internal connections so as to be more likely to produce a correct or sensible answer in future when presented with an input pattern. Linearly Separable and Inseparable ProblemsTo understand these tasks, we have to imagine a network that has to classify two inputs, which I shall call X and Y. Let's suppose that the network must produce an output of 1 if X is bigger than Y, and a 0 otherwise. We can display this task in the form of a graph. Construct an X-Y graph and mark all the points on the graph where X is bigger than Y with a 1 and all the points where X isn't bigger than Y with a 0: 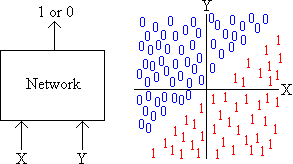 You can easily see that we can draw a straight line that separates all the 1s from all the 0s - it's a diagonal line through the origin (the 0-0 point) of the graph. This is termed a "linearly separable task" - the two regions can be separated by a single straight line. The same would apply if we had three inputs (X, Y and Z). In this case, we couldn't represent them on a flat graph - we would have to use a 3-D cube, but as long as we could cut off all the 1s from the 0s with one straight line cut, then it would be a linearly separable problem. The same thing applies to higher dimensions - four, five, six dimensions etc. Here, we wouldn't be able to draw them on a graph (or even imagine them in our heads - our visual imagination doesn't stretch to 4 dimensions or higher), but we can still consider them mathematically. What about a linearly inseparable task, then? Well, let's alter the task our network has to cope with. Let's ask it to give a 1 only when X and Y have different signs (i.e. when X is positive and Y is negative, or vice-versa). This time, the graph would look like this: 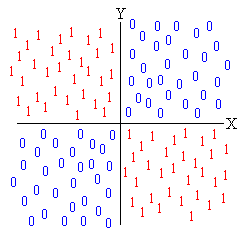 This time, you can't separate all the 1s from all the 0s with only one straight line. This problem is "linearly inseparable", and harder for neural networks to solve. The simpler types of neural network, such as Hebbian nets and single-layer perceptrons, can classify linearly separable tasks but not linearly inseparable ones (they keep getting the answer wrong!) More complicated networks, such as multi-layer perceptrons, can classify linearly separable tasks, but they require more training to get the answer consistently right. Receptive FieldThe receptive field of a cell is the set of all cells that feed input into it. For cells in a standard Multi-Layer Perceptron, each cell gets input from all the cells in the layer beneath it (or the input itself), i.e. the receptive field of a cell is all the cells in the layer beneath. However, in some architectures, input to cells is restricted to only some of the cells in the layer beneath, and so we say that those cells have a restricted receptive field. Recurrent NetworksA recurrent net is a neural network with feedback links. The signal can travel round in loops. Recurrent nets have memory - their output depends not only on the current input, but also on this old signal that has passed round the loop. Supervised and Unsupervised trainingNeural networks, whatever their layout, contain connections between nodes. These connections have certain strengths - indeed, the knowledge is stored in the pattern of weights - and these weights have to be set up somehow. The process of acquiring the correct strengths is called training. There are two types of training. With supervised training, the neural network is given patterns that it is supposed to learn together with the output pattern that it is supposed to produce. Some human must go through the training data and label each pattern with the correct response that the network must make. In the case of unsupervised training, the network is given a large number of patterns, but is not told what it is supposed to produce in each circumstance. You might think that it couldn't possibly learn anything, but there are some types of neural network (e.g. Kohonen's Self-Organising Feature Maps) that can learn to organise the input patterns into groups, and classify similar patterns in a similar way. It might, for instance, learn that all the male faces belong in one category while all the female faces belong in another - even though it couldn't actually put names to those categories. XOR ProblemSee Exclusive Or Problem. |

Main menu
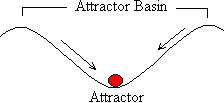 Here's an analogy. Suppose you had a landscape with several hills and valleys. If you drop a smooth boulder somewhere on one of the hills, it will roll down into a valley basin and stop when it reaches the lowest point. There a large number of points on the hillside where you could drop the boulder for it always to end up in the same place. That's why they call it a basin!
Here's an analogy. Suppose you had a landscape with several hills and valleys. If you drop a smooth boulder somewhere on one of the hills, it will roll down into a valley basin and stop when it reaches the lowest point. There a large number of points on the hillside where you could drop the boulder for it always to end up in the same place. That's why they call it a basin!